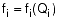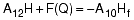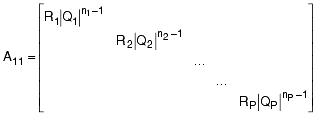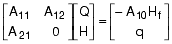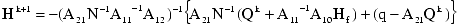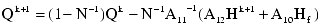假定存在一个由 N 个未知水头节点、P 个未知流量链路和 B 个边界或固定水头节点定义的管网，管网拓扑可以用两个关联矩阵表示：

和

以下约定用于分配矩阵值：

分配的节点需水量的计算公式如下：

分配的边界节点水头的计算公式如下：

水头损失或增益转换采用以下矩阵表示：

定义已知或迭代管网状态的这些矩阵元素可用于计算由未知流量和未知节点水头的矩阵量表示的最终恒稳态管网。

未知链路流量的定义公式如下：

未知节点水头的定义公式如下：

这些拓扑和数量矩阵可以使用能量和质量守恒定律公式化为广义矩阵表达式：

引入了另一个实现矢量化水头变化系数的对角矩阵。在这种情况下，针对海森-威廉摩擦损失进行了泛化：

这会得到矩阵形式的管网响应完整表达式：

要求解非线性方程组，可以通过对方程两边的 Q 和 H 进行求导来获得牛顿-拉夫逊迭代方案，并得到：

具有

牛顿-拉夫逊算法的最终递归形式现在可以在矩阵反演和各种代数操作和替换（这里不介绍）之后推导出。每个解迭代 k 的工作方程组的计算公式如下：

每次迭代的每个未知节点水头的解涉及巨大的计算量。该高速求解利用专门为此矩阵方程组的结构定制的高度优化的稀疏矩阵求解器。

来源：

Todini, E. 和 S. Pilati，“管网分析的梯度算法 (A gradient Algorithm for the Analysis of Pipe Networks)”，《计算机在供水中的应用，第 1 卷 - 系统分析与模拟》，由 Bryan Callback 和 Chin-Hour Or 主编, Research Studies Press LTD，莱奇沃思，赫特福德郡，英格兰。